
○中高一貫の教材の系統性


中高一貫の数学の年間指導計画を編成していく際に、各発達段階によって分けられている内容、領域を6年間を通して概観していく必要がある。このことにより、意図的、継続的な指導が効果的に働くと考えたからである。
1 中学校の領域
中学校学習指導要領によると、中学校では、数学の領域を「数と式」「図形」「数量関係」の三つに分けている。
2 高校の領域
高校では、領域構成をしていない。各科目をいくつかの内容で構成している。
概観すると下記のようになる。
| 科目 | 内 容 |
| 数学Ⅰ | ○方程式と不等式 ○二次関数 ○図形と計算 |
| 数学A | ○平面図形 ○集合と論理 ○場合の数と確率 |
| 数学Ⅱ | ○式と証明・高次方程式 ○図形と方程式 ○いろいろな関数 ○微分・積分の考え |
| 数学B | ○数列 ○ベクトル ○統計とコンピュータ ○数値計算とコンピュータ |
| 数学Ⅲ | ○極限 ○微分法 ○積分法 |
| 数学C | ○行列とその応用 ○式と曲線 ○確率分布 ○統計処理 |
3 中高一貫の領域の考え方
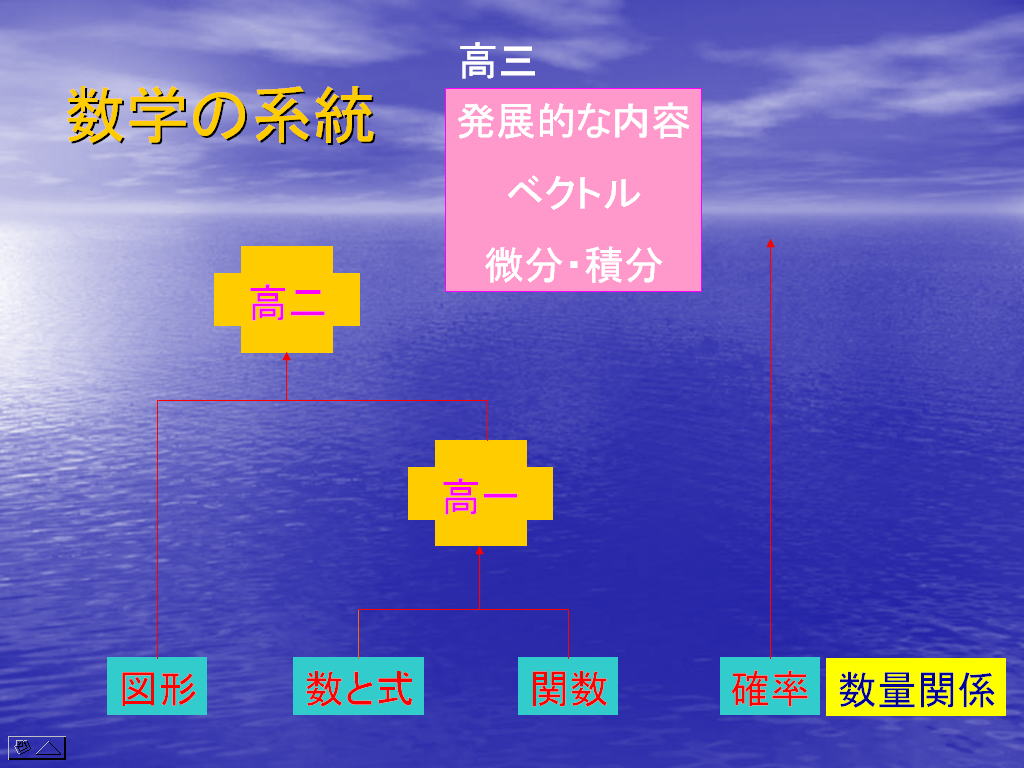
中学校、高校と三年ずつで区切っていた系統性を六年間を通してみると、次のようになる。
①高校一年生の数学Ⅰ、二次関数(y=ax2+bx+c)のグラフで、中学校の領域「数と式」と「関数」が一緒に扱われる場面が出てくる。
②高校二年生の数学Ⅱ、円の方程式(x2+y2+ax+bx+c=0)のグラフで、①に加えて、図形が一緒に扱われる場面が出てくる。
③高校二年生の数学Ⅱで、発展的な内容が扱われ始める。
・直交座標の空間での数学の扱いが終わり、ベクトルを通した、直交座標でない場合の数学的な表現が扱われる。
・微分、積分の考えを通して、極限や変化率に対する考えを深める。
④確率は、六年間を通して、最後まで独立した内容を形成している。数学Cの確率分布で、積分とのかかわりが出始めるが、大学数学を待たないと内容は深まらない。
以上のことを基に、系統性をまとめると下のようになる。
| 平方根 | 13時間 | 中高一貫の年間指導計画では、高校受験に対策を講じる必要が無くなるため、三年生の段階で精神的なゆとりが生じる。 105-86=19 19時間のゆとり 中学校三年生の年間指導計画へのリンク 資料6 中高間の接続について 資料6 年間指導計画3年 |
| 多項式(展開) | 10時間 | |
| 因数分解 | 9時間 | |
| 二次方程式 | 11時間 | |
| 相似 | 10時間 | |
| 平行線と比 | 9時間 | |
| 三平方の定理 | 11時間 | |
| 二次関数 | 13時間 | |
| 合計時数 | 86時間 |
| 基礎期(1・2年生) | 充実期(3・4年生) | 発展期(5・6年生) | |
| 生徒の実態 | ○ある程度能力の等しい集団 ・得意な生徒は得意にする。 ・苦手な生徒は普通にする。 |
○個人差が開く ・理解力の差 ・課題を解決する速さの差 |
○数学を選択しない生徒 ・理系、文系、 ・海外の大学 |
| 手 だ て |
○生徒一人一人の能力を伸ばすための手立ての投入 ・コミュニケーション活動 ・数学的な活動 ・導入の手だて |
○自分の能力に応じたコースの選択 ・習熟度別 (フェルマーコース) (ユークリッドコース) |
○数学の概念形成 ○元になる概念の活用 ○活用される概念 ○評価の観点 |
○手だての説明
<基礎期(1・2年生)>
| コミュニケーション活動 | 自他の追求方法や追求結果を、簡潔さ、明瞭さ、的確さなどを観点に比較したり、共通点や相違点を考えたり、一般性の追求方法や追求結果を求めたりする活動 |
| 数学的な活動 | 単にできあがった数学を知るのではなく、事象を観察して法則を見付けて事柄の性質を明らかにしたり、具体的な操作や実験を試みることを通して数学的内容を帰納したりして、数学を創造し発展させる活動を通して数学を学ぶことを経験させ、その過程の中に見られる工夫、驚き、感動を味わい、数学を学ぶことの面白さ、考えることの楽しさを味わえるようにすることが大切である(中学校学習指導要領) |
| 導入の手だて | 単元の最初や最初の複数時間内では、生徒が必要感や見通しがもてるように次のような活動を取り入れることにした。これらの活動は、より多くの活動を組み合わせて取り入れることでより効果が上がると考えている。 ・日常生活と関連のある活動 ・必要感のもてる活動 ・日常の事象の中から類似したり対照であったりする複数の事象を比較する活動 ・複数の立体や平面を仲間分けする活動 ・「おやっ」と思えるようなゲーム的な活動 ・多様な追求方法や追求結果が現れるような活動 ・単元の見通しがもてるような活動 ・操作を通して秘密(性質)が見付けられるような活動 |
<充実期(3・4年生)>
| 生徒一人一人に応じた学習を展開しようと思っていても、個人差が開いてくることが予想される。その個人差は、理解力の速さの差、提示された課題を解決する速さの差となって外部には現れる。少人数学習では、習熟度別学習も成果があることがいわれている。 中等教育学校の生徒たちは、ある程度同じような能力をもった生徒であることが期待できるが、時間の経過と共に、得意な生徒数学が好きな生徒は、その反対の生徒たちより、大きな伸びを示し、結果として能力の差の開きが大きくなることが予想される。1・2年生のうちは、等質集団に分けておくことの方がメリットが大きいとしても、3・4年生になれば、習熟度別にして、かなりできる生徒はよりもっとかなりできるようにできる生徒もよりできるようにして行く必要があると考えた。、 そこで、フェルマーコースとユークリッドコースを設定した。フェルマーコースの方が、質、量ともに多くの内容を含むようにした。しかし、単元の内容の進度差が大きくなり過ぎてしまうと、ユークリッドコースの生徒たちが劣等感をもってしまうことを防ぐため、単元ごとの時間数は同じになるように配慮した。 |
<発展期(5・6年生)>
| 5・6年生になると数学を選択しない生徒もいる。文系・理系・海外の大学進学と将来の進路を基に三つの進路が考えられる。この5・6年生の年間指導計画は、四年制大学の理系進学を念頭に置いてつくられている。 5・6年生の年間指導計画の中には、特に「評価計画」を取り入れることにした。 5・6年生になると概念形成も重要であるが、元になる概念を活用して課題を解いていくことがより重要になってくる。概念を活用するためには、それぞれの課題や時間の中で、基になる概念、活用される概念が明確になっておかなければならないと考えた。その概念を評価計画として位置付けておき、この概念が上手に活用できているかを評価しながら授業を進めることで、生徒に主体的な学習をうながすことができると考えた。 |
詳しい年間指導計画についての問い合わせは、下記のメールを使って問い合わせください。
![]() 年間指導計画の問い合わせ
年間指導計画の問い合わせ